How to Estimate Your Car's Coefficient of Rolling Resistance
When
two objects in contact with each other slide, a friction force develops resisting
the motion. In classical physics, we distinguish between static friction (which
resists the onset of motion as some force is applied) and kinetic friction
(which resists movement after it has begun). You’ve noticed this before: the
last time you tried to push a heavy box across the floor, say, you had to give
it a push to get started and overcome the static friction (and if the static
friction was great enough, it perhaps tipped over instead of sliding). When
you stopped pushing, it didn’t continue sliding indefinitely; it gradually
slowed and required some force to keep moving (although not as much as it took
to get started). In both scenarios, your pushing on the box was
required to overcome its static or kinetic friction.
 |
| Upright, the fluid-filled can slides when pushed but as energy is dissipated due to friction with the table surface, it quickly comes to a stop. |
Cars
are a bit more complicated because most of the time the tires don’t just slide relative to the ground, they roll as well. So, to model the resistance force
that opposes a car’s motion due to its contact with the road we don’t use
simple friction but rolling resistance. This approximates not just the tires’
friction with the road but also the tendency of all the spinning things on the
car—tires, wheels, brake rotors, wheel bearings, axles, transmission
components—to not want to rotate due to their angular
inertia and internal friction.
Similar to the historical derivation of the model equation for aerodynamic drag (over time, scientists deduced from measurement that drag was proportional to the square of velocity, fluid density, etc.), we know
from centuries of empirical data that the rolling resistance of wheeled objects
such as cars is proportional to their weight. Mathematically,
…where
CRR is a proportionality
constant called the “coefficient of rolling resistance.” CRR of a typical car on smooth pavement is
generally in the range 0.010-0.020 and for most purposes can be estimated based
on what type of tire is on the car: LRR tires on the low end, non-LRR highway
all-seasons in the middle, softer summer tires and all-terrains at the high end.
(You
might notice I’ve changed weight here to “effective weight,” as some SAE
textbooks suggest. This is an estimated weight based on addition of some
penalty, usually 2-3%, to account for the angular inertial moments I mentioned
above. We’ll see below that this does not matter for purposes of the testing I’ve
developed here).
Second,
aerodynamic drag is proportional to the square of velocity.
Plot
both as a function of velocity and you can see where a good speed range might
be if you want to minimize or maximize the effect of one or the other on
measurements:
 |
| The sum of these, marked in green, is the “road load” plot for my car, or the resistance force it must counter to drive at any speed. |
Et
voilá:
a formula for calculation of CRR from experimental data.
Reality
Bites
I
searched in vain for a stretch of road long enough (~300 ft or longer for my
Prius), flat enough, and level enough to do this test. You can check for these
by coasting your car at low speed in both directions on a candidate road. If it
holds speed or speeds up in one direction and slows in the other, the road is
not level. If it speeds up and slows down in the same direction, the road is
not flat. To use this test, you will need a perfectly flat, perfectly level
road; any slope or undulation at all will induce a drag or thrust force on the
car larger than the rolling resistance we’re trying to measure.
No
matter where I tried, no road around here proved to be suitable. Even smooth parking
lots I thought might work turned out to have measurable slope or undulations. In the end, I gave
up. Oh well, it was a nice idea in theory. You might have better luck,
especially if you have access to something like an airport runway or automotive test track.
A
Simpler Method
The
failure of my initial method to pan out prompted me to consider other ways in
which a person might measure the rolling resistance of their car at home.
Finally, it dawned on me and, after several rounds of testing and fiddling with the procedure, I came up with the following.
To
do this, you simply need a small space—like a parking spot or a garage—that has
a slight slope to it, with enough room to let your car roll a few feet. After
warming up your car by driving it for a while, stop in the parking spot with
the nose toward the downhill direction. Then shift to neutral, lift your foot
off the brake pedal, and observe whether the car begins rolling forward or not.
Before or after doing the roll test, measure the slope of the pavement. Take
the sine of that angle: if your car rolled, this value is greater than CRR,
and if it didn’t roll, it is less than or equal to CRR.
The
warmup is important because CRR is not constant, even if
approximating it as such is usually good enough for predicting performance (as
in the plots above). For example, I tried this with my truck in the garage first
thing the other morning. Cold, it did not roll, which means it had CRR
> 0.019, based on the slope of the floor on that side of the garage. After
running some errands around town, I tried it again with the truck warm. This
time, it rolled—so, CRR < 0.019. I’ll have to wait until
winter to try this in different ambient temperatures, but I expect to find seasonal
variation based on outside air temperature as well.
How
does this work, physically? Since weight always acts vertically, on an incline
there will be a weight component along the car’s horizontal body axis trying to
move it. If this weight component is smaller than the rolling resistance, the
car won’t move; if it is larger, the car will roll. The body-frame horizontal weight
component, Wx, is given by
But
we can do better. If the car moves, it will accelerate from its resting state.
We can model this acceleration mathematically by relating it to the two
opposing forces:
Note
the similarity between this and the equation we derived in the first part for CRR:
they are identical apart from the sine term, which is simply an artifact of the
slope. You might notice that I have included a small angle approximation in this setup and derivation (see if you can determine where); I found that this only affected the final result after the 6th decimal place so I think it's fine to use here.
Thus,
if we can measure the acceleration of the car then it should be possible to
calculate CRR. You can do this using an app
on your smartphone like Physics Toolbox or another that can read the phone’s
accelerometer. Open the app and slide the phone in various directions to
determine which is the x-axis, which the y-axis, and which the z-axis. Looking
at the screen on my phone, +x is to the left side, +y to the top,
and +z out the back. The relationship between these axes follows the right-hand
rule and should be the same on any phone (because any one
axis is the cross product of the other two, or the vector orthogonal to
both), so once you determine the positive direction of two axes you can find
the last pretty easily.
In
the car, align one of the phone’s axes with the car’s longitudinal body axis. I
chose to use x, following aerospace convention (+x out the front
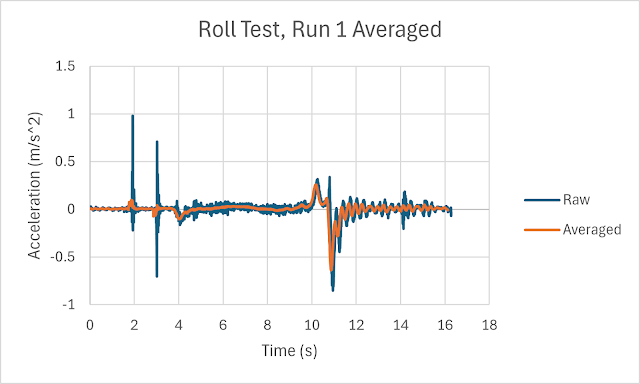
of the car, +y to the right, and +z down) by taping the phone to the dash sideways after checking that it showed the same angle as the floor. It's important that the phone be fixed to the car as securely as possible. Any relative movement between the phone and car will show up in the measured acceleration, as I found in initial testing (you can still see it in the plots below as a negative spike when the car begins rolling and a corresponding positive spike when the brake is applied). It's impossible to eliminate this, but try and minimize it as much as possible by taping the phone down or otherwise fixing it to the car. We're trying to measure the car's acceleration here, not the phone's.
Set the app to show linear acceleration
and record the axis that aligns with the car’s motion. If the app allows
calibration, do that now to zero out the accelerometer while the car is at
rest. Then, hit record, shift to neutral, pause for a beat, and let your foot
off the brake. I found the waiting important; watch the display on your phone to ensure that the accelerometer shows zero between events so you can identify them easily when you plot the data. You should get output that looks like this:
|
|
a (m/s2) |
CRR |
|
Run
1 |
0.032565 |
0.0149860 |
|
Run
2 |
0.031525 |
0.0150920 |
|
Run
3 |
0.027335 |
0.0155191 |
|
Run
4 |
0.033365 |
0.0149044 |
|
Run
5 |
0.017780 |
0.0164931 |
|
Run
6 |
0.026910 |
0.0155624 |
|
Average |
0.028247 |
0.0154262 |
Look at the "roll" portion of the acceleration plots above (I only posted the one but all 6 runs look similar) and you can see that rolling resistance isn't constant and slowly varies as the car rolls forward. Again, there are real effects not accounted for in the model. Should that be reason for concern? Yes and no. "Yes" because the real rolling force is not quite constant, and if you want to be as exact as possible in modeling it or measuring it this variability should be accounted for. "No" because, for most engineering purposes, the variability is small enough that it can probably be neglected. I had a professor this past semester who said in class as we were working through a derivation and throwing in a small angle approximation, "We're engineers, not scientists." This is the explanation of the famous joke that, to an engineer, π = 3. Most of the time, that's close enough.
Finally, the "brake applied" portion of the graph also shows something interesting. You might have noticed already, but constant brake application produces an acceleration plot that looks very similar to a damped spring-mass system. Again, all six plots look like this, so it isn't an aberration. I'll investigate this in future, since I'm not sure if it's an artifact of the overly sensitive accelerometer on the phone or something physical in the car's braking behavior.
Reducing Rolling Resistance







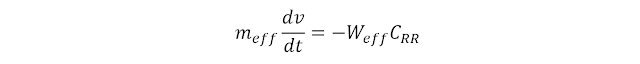











Comments
Post a Comment